Die Investitionsrechnung soll die finanzielle Auswirkung einer Investition prognostizieren, um eine Investitionsentscheidung treffen zu können. Im Grunde geht es um die Frage "Ist die Investition günstiger als die Nicht-Investition?"
1. Statische Verfahren
Die statischen Verfahren der Investitionsrechnung betrachten zwar die zeitliche Komponente, verzichten allerdings auf eine Auf- bzw. Abzinsung und treffen generell vereinfachte Annahmen. Dafür sind diese Methoden entsprechend einfach und schnell anzuwenden und werden dementsprechend häufig in der Praxis angewandt.
Es werden folgende grundlegenden Methoden unterschieden:
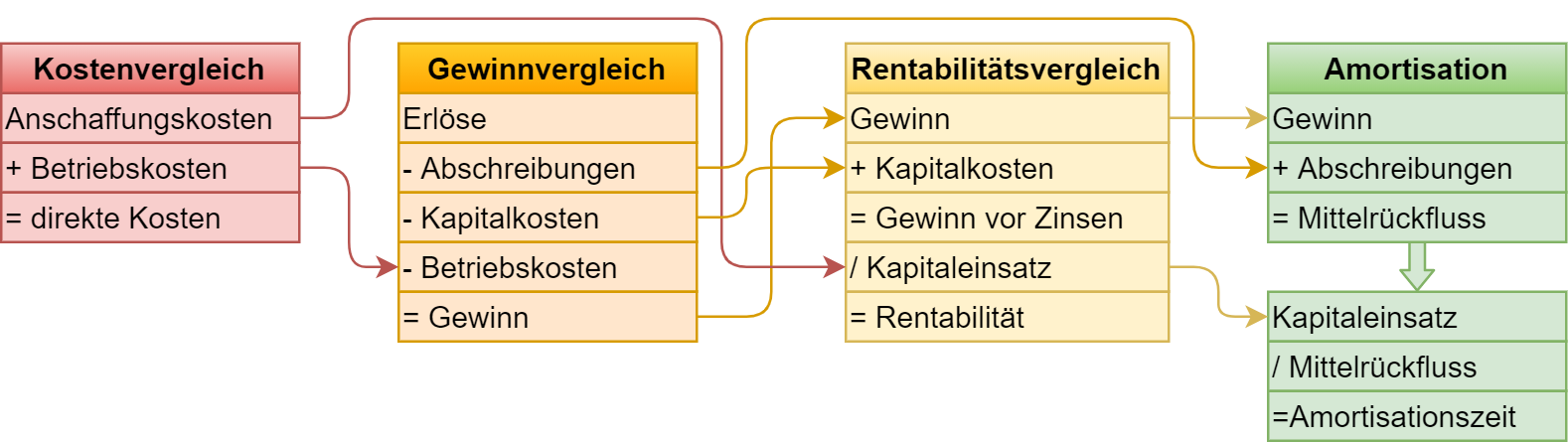
1.1. Kostenvergleichsrechnung
Direkter Vergleich der Kosten zweier oder mehr Alternativen.
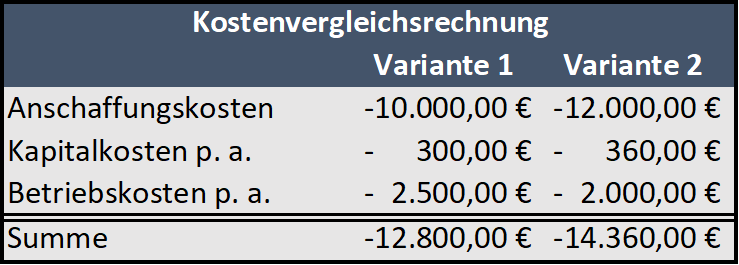
1.2. Gewinnvergleichsrechnung
Direkter Vergleich der prognostizierten Gewinne (abzüglich der Kosten) zweier oder mehr Alternativen.
- Zu beachten
-
\$"Kapitalkosten" = "Darlehenssumme" / 2 * "Zinssatz"\$
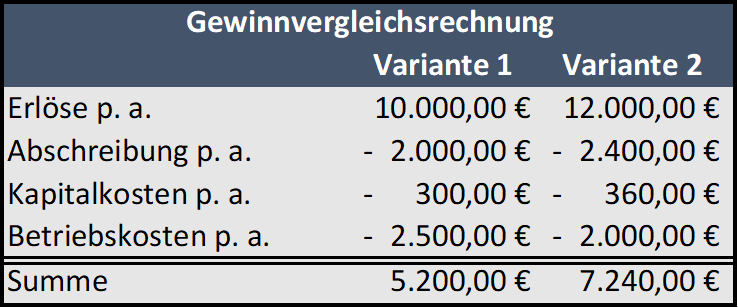
1.3. Rentabilitätsvergleichsrechnung
Direkter Vergleich der prognostizierten Gewinne, ins Verhältnis zu den eingesetzten Mitteln gesetzt. Die Zinsen werden wieder eingerechnet, um einen von der Finanzierung unabhängigen Vergleich zu schaffen.
- Zu beachten
-
\$"Kapitaleinsatz" = ("Anschaffungskosten" + ("Anschaffungskosten" / "Nutzungsdauer"))/2\$
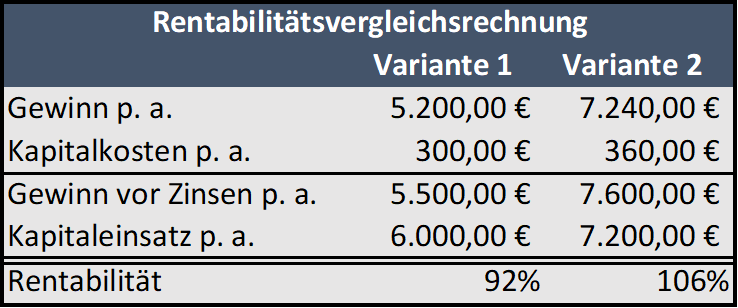
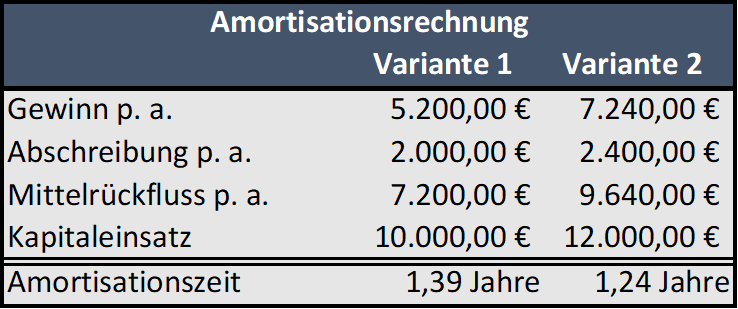
1.4. Amortisationsrechnung
Einnahmen kumuliert den eingesetzten Mitteln gegenüberstellen. Abschreibungen sind nur kalkulatorisch, müssen also, um den tatsächlichen Geldfluss (Cashflow) zu ermitteln, wieder dazugerechnet werden.
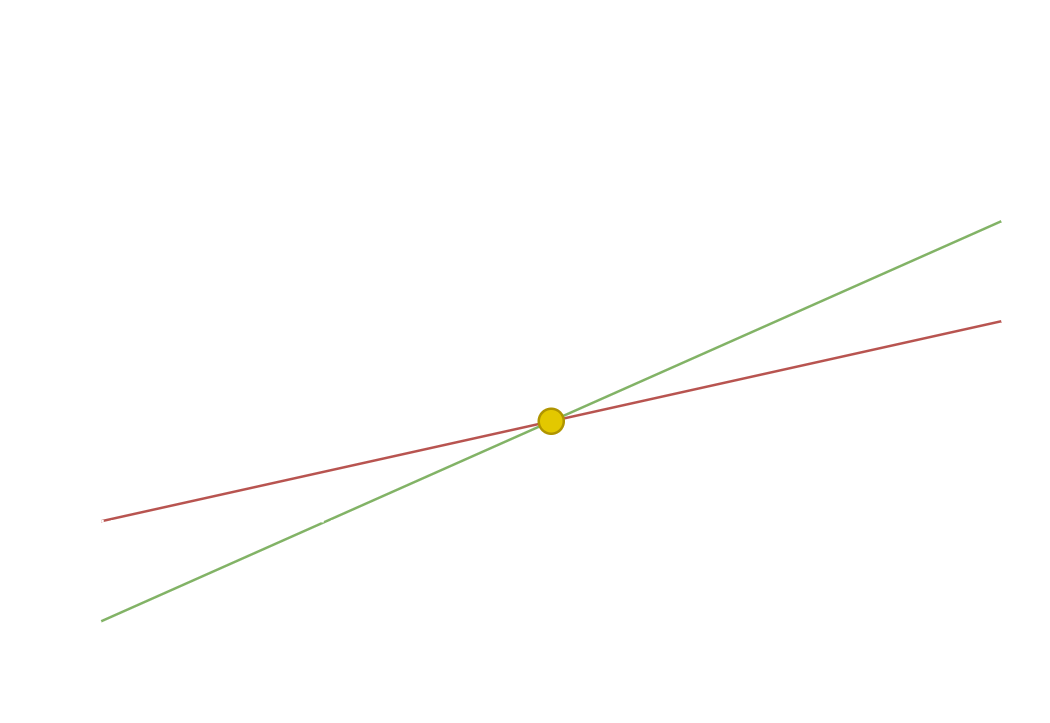
1.5. Break-Even-Analyse
Der sogenannte Break-Even-Point ist Verkaufsmenge, an der die Kosten vollständig von den Erlösen gedeckt werden und das Ergebnise in die Gewinnzone gelangt. Die Kosten werden dabei als Gesamtkosten aus fixen Investitionskosten und variablen Stück- oder Betriebskosten betrachtet.
- Rechenformel
-
- Seien
-
\$"BEM" = "Break-Even-Menge"\$
\$K_"fix" = "Fixkosten"\$
\$K_"var" = "variable Kosten"\$
\$P = "Stückpreis"\$ - Dann gilt
-
\$"BEM" = K_"fix" / ("P" - K_"var")\$
2. Dynamische Verfahren
Die dynamischen versuchen die Rendite der Investition vergleichbar zu machen mit einer Investition am Kapitalmarkt zum gleichen Zeitpunkt. Basis dafür ist der Zins, den man zum Zeitpunkt der Berechnung im Schnitt mit einem Investment am Kapitalmarkt erzielen kann.
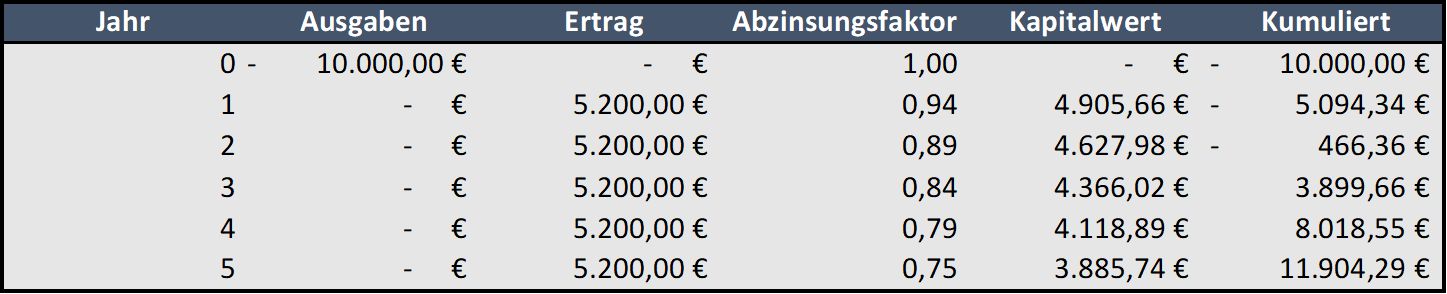
2.1. Kapitalwertmethode
Aufgrund von Verzinsung hat jeder Geldbetrag einen umso höheren Wert, je eher man ihn erhält. Dieser Umstand wird hier über eine Abzinsung dargestellt, die jedes Jahr größer ausfällt, da die Einnahmen ja zu einem umso späteren Zeitpunkt verfügbar sind. Damit wird versucht den Vergleich mit einer Investition am Kapitalmarkt zu simulieren, bei der das Geld entsprechend verzinst wird.
Für die Abzinsung wird aus den verfügbaren Daten ein sogenannter Abzinsungsfaktor errechnet, mit dem die verrechneten Einnahmen des jeweiligen Jahres multipliziert werden.
- Berechnung des Abzinsungsfaktors
-
- Seien
-
\$Z_t = "Cashflow zum Zeitpunkt " t\$
\$t = "Jahr"\$
\$r = "Zins"\$ - Dann ergibt sich für die Summe der Investitionen
-
\$Z_0 + sum_(t=1)^TZ_t/(1+r)^t\$
- Daraus ergibt sich für jedes Jahr
-
\$Z_t/(1+r)^t = Z_t 1/(1+r)^t\$
- Der Abzinsungsfaktor ist also
-
\$1/(1+r)^t\$
2.2. Interne Zinsfußmethode
Mit der Zinsfußmethode lässt sich aus der Differenz zweier Cashflows zu verschiedenen Zeitpunkten der Abzinsungsfaktor (zumindest grob) errechnen. Damit lässt sich eine theoretische mittlere Rendite für das betrachtete Jahr ermitteln.
Der ermittelte Abszinsungsfaktor kann selbstverständlich auch in der Kapitalwertmethode genutzt werden.
- Berechnungsbeispiel
-
- Gegeben sei die Formel
-
\$0 = t_0 + 1/(1+i)t_1\$
\$<=> 1+i = t_1/t_0\$ - Und seien
-
\$t_0 = -100000"€"\$
\$t_1 = 1100000"€"\$ - Dann ergibt sich
-
\$1+i = (110000"€")/(100000"€")\$
\$<=> i = 0,1\$
\$=> 10% "Zinsen"\$